Supplementary Information for The Carbon Abatement Potential of High Penetration Intermittent Renewables
|
|
|
- Elfrieda Norton
- 5 years ago
- Views:
Transcription
1 Supplementary Information for The Carbon Abatement Potential of High Penetration Intermittent Renewables Elaine K. Hart a and Mark Z. Jacobson a 1 Model updates A number of improvements were made to the scheduling and dispatch model used in this study since the publication of [Hart and Jacobson(211)]. These changes are described below. 1.1 Wind Power Statistical Model The statistical model for wind power employed in [Hart and Jacobson(211)] relied on the application of a power curve to simulated wind speeds at each site in order to approximate the output of wind power from each farm. This model used a single average wind speed at each time step for each site in order to reduce computational complexity. This approximation was later found to overestimate the wind power produced in aggregate, when compared to the predicted wind power output supplied in the Western Wind Dataset [3TIER(2)]. To improve the treatment of wind power, an autoregressive-like model was developed for the forecast error of the total aggregated wind power output (the sum of the power output reported for each site in the dataset). In the updated model, the normalized aggregated wind power, g(t) is approximated from the forecasted wind power, ĝ(t) according to: g(t) = ĝ(t) + β [g(t 1) ĝ(t)] + ỹ (1) where β is the autocorrelation coefficient of the input wind power signal and ỹ is a random variable with a symmetrically truncated distribution based on a normal distribution with mean and variance σ 2 g. The distribution is truncated in order to ensure that g(t) is on the interval [, 1]. This approach breaks down when one of a Department of Civil and Environmental Engineering, Stanford University, Stanford, CA, 943. Fax: ; Tel: ; ehart@stanford.edu 1
2 the following inequalities holds: ĝ(t) + β [g(t 1) ĝ(t 1)] < (2) ĝ(t) + β [g(t 1) ĝ(t 1)] > 1 (3) If the first inequality holds, g(t) is set to and if the second inequality holds, g(t) is set to 1. In the k th realization, the available wind power, Pw max, is calculated from the k th normalized wind power signal, g(k, t) and the installed capacity, W according to: Pw max (t) = W g(k, t) (4) Capping introduces a small bias in the final wind power signal. This bias is removed by scaling all values of Pw max (k, t) by a constant so that the mean wind power availability across all realizations and all times is equal to the mean forecasted wind power output. The input wind power signal (from the Western Wind Dataset[3TIER(2)]) is taken as the day-ahead forecasted wind power output. The forecast error distribution produced by this method depends on the parameter, σ g. In this analysis, both the wind and solar power forecasts are assumed to have a % day-ahead RMS error. This is achieved for wind power by comparing the RMS wind power error associated with GW of installed wind power for various values of σ g. This analysis (shown in Figure 1) yielded a value of σ g RMS Error of Wind Power Output (%) Standard Deviation of Normalized Wind Power, σ g Figure 1 Wind power forecast error trials for determining σ g. The value of σ g is chosen so that the RMS error of the day-ahead forecast is approximately %. 2 Student Version of MATLAB
3 1.2 Irradiance Statistical Model The updated irradiance model assumes that the forecast error in the direct normal irradiance, I DNI can be modeled by an autoregressive-like process: [ ] Ii DNI (t) = ÎDNI i (t) + κ Ii DNI (t 1) ÎDNI i (t 1) + b i () where ÎDNI i is the forecasted direct normal irradiance at site i, φ is the autocorrelation coefficient, and b i N (, σdni 2 ) are correlated random variables, based on the site-site correlations present in the input dataset. Irradiance data from the National Solar Radiation Database (NSRDB) [Wilcox and Marion(27)] was used in this analysis. At each time step, Ii DNI (t) is capped so that it is necessarily non-negative. After producing all realizations, Ii DNI (t) is again capped so that it never exceeds the maximum observed DNI in each hour of the year, based on data from 1991 to 2. The diffuse horizontal irradiance (DHI) is calculated directly from the DNI, assuming an affine relationship between the two variables that depends on the hour of the year. Several plots of the DHI versus the DNI for given hours of the year (over multiple years and multiple sites) indicated that the relationship is substantially different in low- and high-dni regimes and that the DHI peaks at some DNI, separating the two regime (see Figure 2). The data is therefore separated into two regimes in order to approximate the DHI: { Ii DHI c 1 (t)ii DNI (t) + b 1 (t) Ii DNI (t) I (t) (t) = (6) c 2 (t)ii DNI (t) + b 2 (t) Ii DNI (t) > I (t) where t is the hour of the year; the fit parameters c 1 (t), c 2 (t), b 1 (t), and b 2 (t) are selected using a least-squares fit to the data at all stations over the years ; and I (t) is the value of the DNI corresponding to the maximum DHI in hour t across all years, which serves as an approximation for the boundary between the two DHI regimes. The DHI is also capped between and the maximum observed DHI in each hour of the year over several years of NSRDB data to ensure reasonable values. An example of the resulting fit function for the DHI is illustrated for 12:pm on April th in Figure 2. Note that the data shown reflect only 2-2, but the fits used in the simulations include years as well. With the DNI and the DHI, the global horizontal irradiance (GHI) can be approximated according to: I GHI i (t) = Ii DNI (t)sinβ i (t) + Ii DHI (t) (7) where β is the solar altitude angle, a function of both location and time. Since errors in the GHI are often reported, the GHI is used to choose the value of σ DNI 3
4 NSRDB Data Capped Fit Functions DHI, W/m DNI, W/m 2 Figure 2 Irradiance data at 12:pm on April th at all California sites from the NSRDB over 2-2, plotted with the corresponding two-regime fit described in Eq. 6, with capping of values that exceed the maximum DHI in the dataset. that provides the appropriate day-ahead forecast uncertainty. An analysis of the effect of varying σ DNI on the RMS error of the GHI is shown in Figure 3. A value of σ DNI = 13W/m 2 was chosen so that the RMS error of the GHI over the simulation period was approximately %. 14 Student Version of MATLAB RMSE of GHI (% of max GHI) Input Standard Deviation for Direct Beam Irradiance Model, σ IB (W/m 2 ) Figure 3 Solar thermal power forecast error trials for determining σ IB. The value of σ DNI is chosen so that the RMS error of the day-ahead forecast is approximately %. 4 Student Version of MATLAB
5 1.3 Irradiance Data The simulations in [Hart and Jacobson(211)] used irradiance data from the SolarAnywhere database [Clean Power Research, LLC(2)] for the year 26. However, slight differences in the sunrise and sunset times were found between the models employed for the NSRDB and the SolarAnywhere data. Because the NSRDB historical dataset was used to approximate upper bounds for the DNI and the DHI, this discrepancy led to unrealistic capping of the DNI and the DHI in some hours near the sunrise or sunset over 26. In order to avoid this issue, irradiance data was modeled for 26 in this analysis by scaling each day of the 2 DNI time series data by the ratio of the 26 mean daily GHI to the 2 mean daily GHI and capping with the historical maximum DNI to ensure reasonable values. This method maintains the general meteorological conditions from the 26 dataset, but mimics the cloud-cover temporal patterns from the 2 dataset. 1.4 CSP Constraints The CSP model was also updated in order to better account for the flexibility of the curtailment controls. In real parabolic trough systems, curtailment can be achieved by rotating the mirrors away from the sun, a process that requires movement of several large mechanical parts. It is unlikely that this cumbersome approach would be used for real-time load balancing[mancini(211)], so the model now assumes that reductions in the power sent to the thermal energy storage (TES) system from the solar field are scheduled on a day-ahead basis. The following constraints are included in the scheduling problem to determine the solar thermal curtailment schedule: Scsp(t) η s Scsp(t 1) = Pcol(t) P csp(t), t η turb Pcol(t) η col A ap (j)i col(j, t), t j P csp(t) P max csp, t S csp(t) S max csp, t where Scsp is the scheduled energy stored in the TES system, Pcol is the scheduled power collected from all solar fields (which can be reduced from the maximum available solar power by rotating the mirrors away from the sun), Pcsp is the scheduled power output from all CSP systems, A ap (j) is the aperture area at site j, I col is the forecasted irradiance that can be collected by the parabolic troughs, Pcsp max is the maximum aggregated CSP power block capacity, Scsp max is the maximum energy (8)
6 capacity of the TES system, η S is the efficiency of the storage system, η col is the collector efficiency, and η turb is the turbine efficiency. In real-time, the power sent to the TES system from the collectors, P col, is uniquely determined by the scheduled mirror angle and the realized irradiance, I col. P col can be approximated prior to solving the dispatch problem by assuming that the scheduled mirror angle fixes the ratio of the collected energy to the irradiance: [ ] Pcol P col (k, t) = (t) η col j A η ap(j)i col col A ap (j)i col (k, j, t) (j, t) j = Pcol(t) j A (9) ap(j)i col (k, j, t) j A ap(j)i col (j, t) The CSP model then contributes the following constraints to the dispatch problem: S csp (k, t) η s S csp (k, t 1) = P col (k, t) P csp(k, t) η turb, k, t P csp (k, t) P max csp, k, t S csp (k, t) S max csp, k, t where k is the realization and the circle superscript is dropped to indicate that the variables represent realizations or real-time dispatch, rather than schedules. 1. Reserve Capacity Requirements In [Hart and Jacobson(211)], the majority of the carbon emissions associated with high penetrations of renewables were associated with the spinning reserves required to meet the loss of load expectations constraint of 1 day in years. The initial simulations assumed that a constant capacity of spinning reserves was required in every hour of the simulation (unless the reserves exceeded the forecasted load). While the resulting spinning reserve capacities far exceed the present day conventions for spinning reserves, this assumption was made in order to ensure a conservative approximation of the carbon emissions reductions associated with intermittent renewables. Furthermore, it is likely that in systems with high penetrations of intermittent renewables, the present day conventions will not ensure system reliability as they do today. New conventions, which will undoubtedly depend on the penetration of intermittent generation, must be developed for high penetration systems. Toward this end, we have included a new treatment of spinning reserves in the simulations presented in this study. The model assumes that the system operator schedules spinning reserves to be available based on the solution of the day-ahead scheduling problem. Available () 6
7 spinning reserves in each hour, P spin, are assumed to be a linear function of the forecasted load, L, and the scheduled generation from intermittent renewables: P spin(t) = x L L (t) + x R [ P w (t) + P csp + P pv(t) ] (11) where P w is the scheduled wind power, P csp is the scheduled CSP power, and P pv is the forecasted PV output, and x L and x R are constants. Spinning reserve signals are produced for various values of x L and x R and these signals are compared against the power deficit signal (P δ (k, t), an expensive power source included in the dispatch model to ensure feasibility) in order to count the frequency of loss of load events. If the spinning reserve signal is sufficient to meet the power deficit signal in all but.274% of the hours (an LOLE of 1 day in years) across all realizations, then the corresponding x L and x R pair represent an acceptable spinning reserve scheduling strategy. The set of all acceptable spinning reserve strategies, X is therefore described by Equation 12. X = {(x L, x R ) : {(k, t) : P spin (t) P δ (k, t)} LOLE K T } (12) Of all acceptable sets of x L and x R, the strategy is then chosen that minimizes the time-integrated spinning reserve capacity. minimize subject to T t=1 P spin(t) (x L, x R ) X (13) 2 Selection of the flexible generation parameter The deterministic scheduling problem includes a constraint on the maximum amount of scheduled generation, (1 α), in each hour that is allowed to come from inflexible generators. Here, an inflexible generator refers to any technology that cannot be ramped down or curtailed in real-time. The model assumes that geothermal, CSP, PV, and hydroelectric generators are inflexible in this capacity so that all downward flexibility must be provided by flexible natural gas plants and curtailable wind power. These assumptions ensure that the solutions do not underestimate the natural gas capacity required to reliably meet demand or the emissions associated with the generation of natural gas plants. However the flexibility assumptions also neglect some potential contributions to system flexibility from hydroelectric plants. The minimum fraction of scheduled generation that must be downwardly flexible (ie. from wind or natural gas), α is an operating decision that affects both 7
8 the scheduling and the dispatch of the inflexible generators. For systems with CSP, where curtailment of the collected power can be scheduled on a day-ahead basis, a large α will result in CSP curtailment at lower system-wide CSP capacities, while a small α may lead to infeasibility in the dispatch problem in hours of unexpectedly high irradiance. For technologies with uncontrollable output (distributed photovoltaics and baseload generators), a large α may result in infeasibility of the scheduling problem at lower system-wide installed capacities of the technology, while a small α may lead to infeasibility in the dispatch problem in hours of high irradiance and/or low demand. For the single-technology analyses, the sensitivities of the primary model outputs (energy penetration of the technology of interest, system-wide emissions, and total natural gas capacity) to α were investigated for low, moderate, and high capacities. These analyses were used to determine values of α for each technology that minimized the system-wide carbon dioxide emissions while ensuring the feasibility of both the scheduling and dispatch problems. Results from the wind power analysis (see Figure 4) indicate that the model outputs are not sensitive to α in modeling wind power integration because wind power can be curtailed on a real-time basis. This dramatically reduces the burden on the rest of the system to provide downward generating flexibility. Based on this analysis, a value of α =.3 was chosen for all subsequent wind power simulations..2! =.3 7 6! =.3 GW 3GW 6GW 6! =.3 GW 3GW 6GW Carbon Intensity (tco 2 /MWh) Wind Energy Penetration (%) Natural Gas Capacity (GW) 4 4. GW 3GW 3 6GW (a) Flexible Generation Fraction,! (b) Flexible Generation Fraction,! 3 (c) Flexible Generation Fraction,! Figure 4 The sensitivity of (a) system-wide carbon intensity, (b) wind energy penetration, and (c) natural gas capacity to flexible generation fraction, α for wind scenarios, with K = 2. Based on these simulations, a value of α =.3 (shown as red dashed line) was chosen for all subsequent wind power simulations. 8
9 Carbon Intensity (tco 2 /MWh).2.2! =.1 GW 3GW 6GW 9GW CSP Energy Penetration (%) ! =.1 GW 3GW 6GW 9GW Natural Gas Capacity (GW) ! =.1 GW 3GW 6GW 9GW.1 (a) Flexible Generation Fraction,! (b) Flexible Generation Fraction,! (c) 3 Flexible Generation Fraction,! Figure The sensitivity of (a) system-wide carbon intensity, (b) CSP energy penetration, and (c) natural gas capacity to flexible generation fraction, α for wind scenarios, with K = 2. Based on these simulations, a value of α =.1 (shown as red dashed line) was chosen for all subsequent CSP simulations..29! =.1 2! =.1 4! =.1 Carbon Intensity (tco 2 /MWh) GW.22 2GW.21 3GW.2 (a) Flexible Generation Fraction,! PV Energy Penetration (%) 2 GW 2GW 3GW 1 (b) Flexible Generation Fraction,! Natural Gas Capacity (GW) 4 3 GW 2GW 3GW 3 (c) Flexible Generation Fraction,! Figure 6 The sensitivity of (a) system-wide carbon intensity, (b) PV energy penetration, and (c) natural gas capacity to flexible generation fraction, α for wind scenarios, with K = 2. Based on these simulations, a value of α =.1 (shown as red dashed line) was chosen for all subsequent PV power simulations. Results from the CSP analysis are shown in Figure. For values of α smaller than those plotted, the dispatch problem is infeasible for some time steps, and for values of α greater than those plotted, the scheduling problem is infeasible. Not 9
10 surprisingly, the sensitivity of each output to α depends on the CSP penetration, as greater penetrations require greater system-wide flexibility. At higher penetrations, the problem is both more constrained and more sensitive to α. Based on these results, a value of α =.1 was chosen for all subsequent CSP simulations. At high penetrations, this is close to the feasibility limit of the dispatch problem, which ensures fairly low-emissions operation. At lower penetrations, the outputs are less sensitive to α and a value of α =.1 still maintains low-emissions operation. Results from the PV analysis are shown in Figure 6. The model outputs were largely insensitive to the value of α, particularly at small-to-moderate sized capacities. At 3GW, a value of α =.1 yielded both the minimum carbon emissions and minimum natural gas capacity, so this value was chosen for all subsequent PV calculations in the single-technology analysis. In the analyses of portfolios containing both wind and solar power, PVs are modeled as curtailable in order to examine very high penetrations. For these simulations, PVs were not included in the inflexible generation fleet and α was set to.3, as in the wind-only simulations. 3 Natural gas utilization in wind-dominated portfolios The natural gas utilization analysis was repeated for a portfolio with 7GW wind, 3GW solar, 9GW geothermal, and existing hydropower in order to test the sensitivity of the conclusions to the make-up of the renewable portfolio. The results are shown in Figure 7. The natural gas scheduling and utilization patterns are very similar between the solar-dominated portfolio reported in the manuscript and the wind-dominated portfolio shown here. The most prominent difference between the two scenarios arises in the diurnal cycle of the natural gas utilization. Both portfolios tend to require more natural gas reserves at night, when solar power is 2 Hour of the Day 2 1 Hour of the Day (a) Day of Year (b) Day of Year Figure 7 The average (a) available, and (b) utilized natural gas generating capacity in each hour of the year for a simulation of the California ISO over 2-26 with a renewable portfolio consisting of 7GW wind, 3GW solar, and 9GW geothermal power. Student Version of MATLAB Student Version of MATLAB
11 unavailable, however this trend is more prominent in the solar-dominated portfolio because the daytime natural gas utilization is reduced due to an excess of day-time solar power. References [Hart and Jacobson(211)] Hart EK, Jacobson MZ. A Monte Carlo approach to generator portfolio planning and carbon emissions assessments of systems with large penetrations of variable renewables. Renewable Energy 211;36(8): [3TIER(2)] 3TIER. Wind integration datasets. integrationdatasets; 2. [Wilcox and Marion(27)] Wilcox S, Marion W. National solar radiation database, : User s manual. Technical Report TP ; National Renewable Energy Laboratory; 27. URL pdf. [Clean Power Research, LLC(2)] Clean Power Research, LLC. SolarAnywhere [Mancini(211)] Mancini T. Operation of parabolic trough solar power plants Personal Communication. 11
Energy & Environmental Science ANALYSIS. The carbon abatement potential of high penetration intermittent renewables. Dynamic Article Links C <
 Energy & Environmental Science Dynamic Article Links C < Cite this: Energy Environ. Sci., 2012, 5, 6592 www.rsc.org/ees The carbon abatement potential of high penetration intermittent renewables Elaine
Energy & Environmental Science Dynamic Article Links C < Cite this: Energy Environ. Sci., 2012, 5, 6592 www.rsc.org/ees The carbon abatement potential of high penetration intermittent renewables Elaine
An Analysis of Concentrating Solar Power with Thermal Energy Storage in a California 33% Renewable Scenario
 An Analysis of Concentrating Solar Power with Thermal Energy Storage in a California 33% Renewable Scenario Paul Denholm, Yih-Huei Wan, Marissa Hummon, and Mark Mehos NREL is a national laboratory of the
An Analysis of Concentrating Solar Power with Thermal Energy Storage in a California 33% Renewable Scenario Paul Denholm, Yih-Huei Wan, Marissa Hummon, and Mark Mehos NREL is a national laboratory of the
WREF 2012: P50/P90 ANALYSIS FOR SOLAR ENERGY SYSTEMS USING THE SYSTEM ADVISOR MODEL
 WREF 22: P5/P9 ANALYSIS FOR SOLAR ENERGY SYSTEMS USING THE SYSTEM ADVISOR MODEL Aron P. Dobos Strategic Energy Analysis Center National Renewable Energy Laboratory Phone: 33.384.7422 Email: aron.dobos@nrel.gov
WREF 22: P5/P9 ANALYSIS FOR SOLAR ENERGY SYSTEMS USING THE SYSTEM ADVISOR MODEL Aron P. Dobos Strategic Energy Analysis Center National Renewable Energy Laboratory Phone: 33.384.7422 Email: aron.dobos@nrel.gov
RELIABILITY AND SECURITY ISSUES OF MODERN ELECTRIC POWER SYSTEMS WITH HIGH PENETRATION OF RENEWABLE ENERGY SOURCES
 RELIABILITY AND SECURITY ISSUES OF MODERN ELECTRIC POWER SYSTEMS WITH HIGH PENETRATION OF RENEWABLE ENERGY SOURCES Evangelos Dialynas Professor in the National Technical University of Athens Greece dialynas@power.ece.ntua.gr
RELIABILITY AND SECURITY ISSUES OF MODERN ELECTRIC POWER SYSTEMS WITH HIGH PENETRATION OF RENEWABLE ENERGY SOURCES Evangelos Dialynas Professor in the National Technical University of Athens Greece dialynas@power.ece.ntua.gr
An Op&miza&on and Monte Carlo Planning Approach for High Penetra&ons of Intermi;ent Renewables
 An Op&miza&on and Monte Caro Panning Approach for High Penetra&ons of Intermi;ent Renewabes Eaine K. Hart and Mark Z. Jacobson INFORMS Annua Mee>ng, Aus>n, TX November 8, 21 STANFORD UNIVERSITY AT M O
An Op&miza&on and Monte Caro Panning Approach for High Penetra&ons of Intermi;ent Renewabes Eaine K. Hart and Mark Z. Jacobson INFORMS Annua Mee>ng, Aus>n, TX November 8, 21 STANFORD UNIVERSITY AT M O
Three Gorges Dam. Renewable Energy
 Three Gorges Dam Renewable Energy Renewable Energy Technologies Hydro Biomass Geothermal Wind Solar heating and thermal electric Photovoltaic (PV) Ocean tidal and tidal current Ocean wave Ocean thermal
Three Gorges Dam Renewable Energy Renewable Energy Technologies Hydro Biomass Geothermal Wind Solar heating and thermal electric Photovoltaic (PV) Ocean tidal and tidal current Ocean wave Ocean thermal
Baja California Sur Renewable Integration Study
 Baja California Sur Renewable Integration Study Carlo Brancucci, Riccardo Bracho, Greg Brinkman, and Bri-Mathias Hodge National Renewable Energy Laboratory Produced under direction of the 21st Century
Baja California Sur Renewable Integration Study Carlo Brancucci, Riccardo Bracho, Greg Brinkman, and Bri-Mathias Hodge National Renewable Energy Laboratory Produced under direction of the 21st Century
Advanced Modeling and Verification for High Penetration PV: Final Report
 Advanced Modeling and Verification for High Penetration PV: Final Report Tom Hoff President, Research and Consulting April 10, 2012 Copyright 2011 Clean Power Research, L.L.C. Acknowledgements Funding
Advanced Modeling and Verification for High Penetration PV: Final Report Tom Hoff President, Research and Consulting April 10, 2012 Copyright 2011 Clean Power Research, L.L.C. Acknowledgements Funding
Accepted Manuscript. Optimal scheduling of thermal-wind-solar power system with storage. S. Surender Reddy
 Accepted Manuscript Optimal scheduling of thermal-wind-solar power system with storage S. Surender Reddy PII: S00-()0- DOI: 0.0/j.renene.0.0.0 Reference: RENE 0 To appear in: Renewable Energy Received
Accepted Manuscript Optimal scheduling of thermal-wind-solar power system with storage S. Surender Reddy PII: S00-()0- DOI: 0.0/j.renene.0.0.0 Reference: RENE 0 To appear in: Renewable Energy Received
COLLINSVILLE SOLAR THERMAL PROJECT
 COLLINSVILLE SOLAR THERMAL PROJECT YIELD ANALYSIS OF A LINEAR FRESNEL REFLECTOR BASED CSP BY LONG-TERM HISTORIAL DATA Report 2 Prepared for RATCH-Australia Corporation This project is supported by funding
COLLINSVILLE SOLAR THERMAL PROJECT YIELD ANALYSIS OF A LINEAR FRESNEL REFLECTOR BASED CSP BY LONG-TERM HISTORIAL DATA Report 2 Prepared for RATCH-Australia Corporation This project is supported by funding
A reduced-form approach for representing the impacts of wind and solar PV deployment on the structure and operation of the electricity system
 A reduced-form approach for representing the impacts of wind and solar PV deployment on the structure and operation of the electricity system Nils Johnson 1, Manfred Strubegger 1, Madeleine McPherson 2,
A reduced-form approach for representing the impacts of wind and solar PV deployment on the structure and operation of the electricity system Nils Johnson 1, Manfred Strubegger 1, Madeleine McPherson 2,
Comparative Costs of Geothermal, Solar, and Wind Generation Based on California Independent System Operator Electricity Market Data
 GRC Transactions, Vol. 41, 2017 Comparative Costs of Geothermal, Solar, and Wind Generation Based on California Independent System Operator Electricity Market Data Ian Warren U.S. Geothermal Inc. Keywords
GRC Transactions, Vol. 41, 2017 Comparative Costs of Geothermal, Solar, and Wind Generation Based on California Independent System Operator Electricity Market Data Ian Warren U.S. Geothermal Inc. Keywords
A Comparison of Wind Power and Load Forecasting Error Distributions
 A Comparison of Wind Power and Load Forecasting Error Distributions Preprint Bri-Mathias Hodge, Anthony Florita, Kirsten Orwig, Debra Lew, and Michael Milligan Presented at the 2012 World Renewable Energy
A Comparison of Wind Power and Load Forecasting Error Distributions Preprint Bri-Mathias Hodge, Anthony Florita, Kirsten Orwig, Debra Lew, and Michael Milligan Presented at the 2012 World Renewable Energy
Optimizing the Generation Capacity Expansion. Cost in the German Electricity Market
 Optimizing the Generation Capacity Expansion Cost in the German Electricity Market Hamid Aghaie Research Scientist, AIT Austrian Institute of Technology Novemebr 2017 1 Motivation Energy-only Market Generators
Optimizing the Generation Capacity Expansion Cost in the German Electricity Market Hamid Aghaie Research Scientist, AIT Austrian Institute of Technology Novemebr 2017 1 Motivation Energy-only Market Generators
Operation Experience of a 50 MW Solar Thermal Parabolic Trough Plant in Spain
 Operation Experience of a 50 MW Solar Thermal Parabolic Trough Plant in Spain Frank Dinter Eskom Chair in Concentrating Solar Power (CSP) and Solar Thermal Energy Research Group (STERG), Department of
Operation Experience of a 50 MW Solar Thermal Parabolic Trough Plant in Spain Frank Dinter Eskom Chair in Concentrating Solar Power (CSP) and Solar Thermal Energy Research Group (STERG), Department of
THERMAL ENERGY STORAGE AS AN ENABLING TECHNOLOGY FOR RENEWABLE ENERGY
 THERMAL ENERGY STORAGE AS AN ENABLING TECHNOLOGY FOR RENEWABLE ENERGY Paul Denholm National Renewable Energy Laboratory 1617 Cole Blvd. Golden, CO, USA e-mail: paul.denholm@nrel.gov Sean Ong National Renewable
THERMAL ENERGY STORAGE AS AN ENABLING TECHNOLOGY FOR RENEWABLE ENERGY Paul Denholm National Renewable Energy Laboratory 1617 Cole Blvd. Golden, CO, USA e-mail: paul.denholm@nrel.gov Sean Ong National Renewable
Concentrated Solar Thermal Power Technology
 Concentrated Solar Thermal Power Technology Prof. G.R. Tynan MANY SLIDES ADOPTED FROM A TALK AT 2005 AAAS MEETING BY E. BOES, NREL And Professor Carlos Coimbra, UCSD-MAE & CER Three Main Solar Thermal
Concentrated Solar Thermal Power Technology Prof. G.R. Tynan MANY SLIDES ADOPTED FROM A TALK AT 2005 AAAS MEETING BY E. BOES, NREL And Professor Carlos Coimbra, UCSD-MAE & CER Three Main Solar Thermal
4 Calculation of Demand Curve Parameters
 4 Calculation of Demand Curve Parameters This section addresses the demand curve for the Alberta capacity market, including the calculations for the components of the demand curve. 4.1 Resource adequacy
4 Calculation of Demand Curve Parameters This section addresses the demand curve for the Alberta capacity market, including the calculations for the components of the demand curve. 4.1 Resource adequacy
Impact of storage in the operation of Hybrid Solar Systems
 Impact of storage in the operation of Hybrid Solar Systems Garcia, Miguel da Fonte Gomes Abstract There has been a growing concern with which energy sources are being used to generate the electricity.
Impact of storage in the operation of Hybrid Solar Systems Garcia, Miguel da Fonte Gomes Abstract There has been a growing concern with which energy sources are being used to generate the electricity.
AR No. # - Solar Thermal
 AR No. # - Solar Thermal Recommendation We recommend installing a solar thermal array on the building roof. This will provide an alternative source for 10% of the facilities energy consumption and reduce
AR No. # - Solar Thermal Recommendation We recommend installing a solar thermal array on the building roof. This will provide an alternative source for 10% of the facilities energy consumption and reduce
Intermittent Renewable Energy Sources and Wholesale Electricity Prices
 Intermittent Renewable Energy Sources and Wholesale Electricity Prices Felix Müsgens, Thomas Möbius FERC and TAI Workshop Washington, October 30, 2015 Motivation How will intermittent renewable energy
Intermittent Renewable Energy Sources and Wholesale Electricity Prices Felix Müsgens, Thomas Möbius FERC and TAI Workshop Washington, October 30, 2015 Motivation How will intermittent renewable energy
Solar power status and perspectives DESERTEC an update. Dr. Bernd Utz Head of the Project Desertec Initiative of the Renewable Energy Division
 Solar power status and perspectives DESERTEC an update Siemens Press Trip Seville, Lebrija April 13, 2010 Dr. Bernd Utz Head of the Project Desertec Initiative of the Renewable Energy Division Siemens
Solar power status and perspectives DESERTEC an update Siemens Press Trip Seville, Lebrija April 13, 2010 Dr. Bernd Utz Head of the Project Desertec Initiative of the Renewable Energy Division Siemens
The Role of AMI and DR in Enabling Island Renewable Integration
 The Role of AMI and DR in Enabling Island Renewable Integration Smart Metering Caribbean Miami, FL February 23, 2012 Matt Lecar, Principal Lavelle Freeman, Principal GE Energy Consulting Outline Unique
The Role of AMI and DR in Enabling Island Renewable Integration Smart Metering Caribbean Miami, FL February 23, 2012 Matt Lecar, Principal Lavelle Freeman, Principal GE Energy Consulting Outline Unique
Cheap solar is great but what do you do with it? Jimmy Nelson, Ph.D. Kendall Science Fellow Union of Concerned Scientists
 Cheap solar is great but what do you do with it? Jimmy Nelson, Ph.D. Kendall Science Fellow Union of Concerned Scientists jnelson@ucsusa.org PV Idealab UC Berkeley 02/28/2014 Four actions to reduce emissions
Cheap solar is great but what do you do with it? Jimmy Nelson, Ph.D. Kendall Science Fellow Union of Concerned Scientists jnelson@ucsusa.org PV Idealab UC Berkeley 02/28/2014 Four actions to reduce emissions
Eastern Renewable Generation Integration Study. Aaron Bloom
 Eastern Renewable Generation Integration Study Aaron Bloom The Largest Coordinated Power System in the World 2 Reliably Designed for Traditional Fuel Sources 3 A System in Transition 4 Unit Commitment
Eastern Renewable Generation Integration Study Aaron Bloom The Largest Coordinated Power System in the World 2 Reliably Designed for Traditional Fuel Sources 3 A System in Transition 4 Unit Commitment
STE/CSP the current cost competitive carbon free choice for evening and night dispatch profile
 STE/CSP the current cost competitive carbon free choice for evening and night dispatch profile Dr. Luis Crespo President of ESTELA President of Protermosolar Common understanding and the big question mark
STE/CSP the current cost competitive carbon free choice for evening and night dispatch profile Dr. Luis Crespo President of ESTELA President of Protermosolar Common understanding and the big question mark
Renewable Energy, Power Storage, and the Importance of Modeling Partitioned Power Markets
 Renewable Energy, Power Storage, and the Importance of Modeling Partitioned Power Markets 2009 GTSP Technical Workshop May 28, 2009 College Park, MD Marshall Wise, Kate Calvin, Page Kyle, Steve Smith Joint
Renewable Energy, Power Storage, and the Importance of Modeling Partitioned Power Markets 2009 GTSP Technical Workshop May 28, 2009 College Park, MD Marshall Wise, Kate Calvin, Page Kyle, Steve Smith Joint
Renewable Energy Technology MJ2411
 Energy Technology EXAMINATION Renewable Energy Technology MJ2411 2015/01/14 14 00-18 00 This exam paper contains five problems. You need to attempt all these problems. Total points allocated for this examination
Energy Technology EXAMINATION Renewable Energy Technology MJ2411 2015/01/14 14 00-18 00 This exam paper contains five problems. You need to attempt all these problems. Total points allocated for this examination
Development of Data Sets for PV Integration Studies
 Development of Data Sets for PV Integration Studies Utility-scale PV Variability Workshop Ray George 7 October 2009 NREL is a national laboratory of the U.S. Department of Energy Office of Energy Efficiency
Development of Data Sets for PV Integration Studies Utility-scale PV Variability Workshop Ray George 7 October 2009 NREL is a national laboratory of the U.S. Department of Energy Office of Energy Efficiency
Calculating a Dependable Solar. Generation Curve for. SCE s Preferred Resources Pilot
 S o u t h e r n C a l i f o r n i a E d i s o n P a g e 1 Calculating a Dependable Solar Generation Curve for SCE s Preferred Resources Pilot October 2017 S o u t h e r n C a l i f o r n i a E d i s o
S o u t h e r n C a l i f o r n i a E d i s o n P a g e 1 Calculating a Dependable Solar Generation Curve for SCE s Preferred Resources Pilot October 2017 S o u t h e r n C a l i f o r n i a E d i s o
RENEWABLE ENERGY SERVICES GRID SOLUTIONS
 RENEWABLE ENERGY SERVICES GRID SOLUTIONS 1 ABOUT US Leaders in Global Services for Renewable Energy UL works to help renewable energy manufacturers, developers, owners, investors, lenders, utilities and
RENEWABLE ENERGY SERVICES GRID SOLUTIONS 1 ABOUT US Leaders in Global Services for Renewable Energy UL works to help renewable energy manufacturers, developers, owners, investors, lenders, utilities and
VIBRANT CLEAN ENERGY, LLC
 RESPONSE TO JACOBSON ET AL. CLAIM THAT THERE ARE MANY 100% RE STUDIES THAT BACK UP THEIR CLAIM TO RELY ALMOST ENTIRELY ON WIND, SOLAR, AND HYDRO Mason et al. (2010): A 100% renewable electricity generation
RESPONSE TO JACOBSON ET AL. CLAIM THAT THERE ARE MANY 100% RE STUDIES THAT BACK UP THEIR CLAIM TO RELY ALMOST ENTIRELY ON WIND, SOLAR, AND HYDRO Mason et al. (2010): A 100% renewable electricity generation
The Influence of Demand Resource Response Time in Balancing Wind and Load
 2013 46th Hawaii International Conference on System Sciences The Influence of Demand Resource Response Time in Balancing Wind and Load Judith Cardell Smith College jcardell@smith.edu Lindsay Anderson Cornell
2013 46th Hawaii International Conference on System Sciences The Influence of Demand Resource Response Time in Balancing Wind and Load Judith Cardell Smith College jcardell@smith.edu Lindsay Anderson Cornell
Hydropower as Flexibility Provider: Modeling Approaches and Numerical Analysis
 Hydropower as Flexibility Provider: Modeling Approaches and Numerical Analysis Andrew Hamann, Prof. Gabriela Hug Power Systems Laboratory, ETH Zürich February 8, 2017 Future Electric Power Systems and
Hydropower as Flexibility Provider: Modeling Approaches and Numerical Analysis Andrew Hamann, Prof. Gabriela Hug Power Systems Laboratory, ETH Zürich February 8, 2017 Future Electric Power Systems and
Wind Resource Quality Affected by High Levels of Renewables
 Resources 2015, 4, 378-383; doi:10.3390/resources4020378 Communication OPEN ACCESS resources ISSN 2079-9276 www.mdpi.com/journal/resources Wind Resource Quality Affected by High Levels of Renewables Victor
Resources 2015, 4, 378-383; doi:10.3390/resources4020378 Communication OPEN ACCESS resources ISSN 2079-9276 www.mdpi.com/journal/resources Wind Resource Quality Affected by High Levels of Renewables Victor
Stochastic simulation of photovoltaic electricity feed-in considering spatial correlation
 Stochastic simulation of photovoltaic electricity feed-in considering spatial correlation Hans Schermeyer, Hannes Schwarz, Valentin Bertsch, Wolf Fichtner Chair of Energy Economics, Institute for Industrial
Stochastic simulation of photovoltaic electricity feed-in considering spatial correlation Hans Schermeyer, Hannes Schwarz, Valentin Bertsch, Wolf Fichtner Chair of Energy Economics, Institute for Industrial
A technique for accurate energy yields prediction of photovoltaic system
 International Journal of Smart Grid and Clean Energy A technique for accurate energy yields prediction of photovoltaic system Chiou-Jye Huang a*, Chao-Yang Huang a,b, Po-Chun Huang a, Shun-Hung Tsai c
International Journal of Smart Grid and Clean Energy A technique for accurate energy yields prediction of photovoltaic system Chiou-Jye Huang a*, Chao-Yang Huang a,b, Po-Chun Huang a, Shun-Hung Tsai c
Integration of variable renewable energy in power grid and industry Cédric Philibert, Renewable Energy Division, International Energy Agency
 Integration of variable renewable energy in power grid and industry Cédric Philibert, Renewable Energy Division, International Energy Agency International workshop on integration & interconnection, Santiago
Integration of variable renewable energy in power grid and industry Cédric Philibert, Renewable Energy Division, International Energy Agency International workshop on integration & interconnection, Santiago
Off-design Performance of the Recompression sco2 Cycle for CSP Applications
 Off-design Performance of the Recompression sco2 Cycle for CSP Applications 5 th International Supercritical CO2 Power Cycles Symposium Ty Neises -NREL Louis Tse -UCLA March 30, 2016 NREL is a national
Off-design Performance of the Recompression sco2 Cycle for CSP Applications 5 th International Supercritical CO2 Power Cycles Symposium Ty Neises -NREL Louis Tse -UCLA March 30, 2016 NREL is a national
Renewable Integration Impact Assessment Finding integration inflection points of increasing renewable energy. NCEP Webinar Sept.
 Renewable Integration Impact Assessment Finding integration inflection points of increasing renewable energy NCEP Webinar Sept. 13 th, 18 Cumulative Renewable Additions (GW) Renewable energy is growing;
Renewable Integration Impact Assessment Finding integration inflection points of increasing renewable energy NCEP Webinar Sept. 13 th, 18 Cumulative Renewable Additions (GW) Renewable energy is growing;
ERCOT Public LTRA Probabilistic Reliability Assessment. Final Report
 ERCOT Public 2016 LTRA Probabilistic Reliability Assessment Final Report November 21, 2016 Contents Summary... 1 Software Model Description... 3 Demand Modeling... 3 Controllable Capacity Demand Response
ERCOT Public 2016 LTRA Probabilistic Reliability Assessment Final Report November 21, 2016 Contents Summary... 1 Software Model Description... 3 Demand Modeling... 3 Controllable Capacity Demand Response
Impacts of High Variable Renewable Energy (VRE) Futures on Electric-Sector Decision Making
 Impacts of High Variable Renewable Energy (VRE) Futures on Joachim Seel, Andrew Mills, Ryan Wiser Lawrence Berkeley National Laboratory Presentation at International Conference on Energy Systems Integration
Impacts of High Variable Renewable Energy (VRE) Futures on Joachim Seel, Andrew Mills, Ryan Wiser Lawrence Berkeley National Laboratory Presentation at International Conference on Energy Systems Integration
Incorporating Flexibility into Long-term Energy System Models
 Workshop on Short term versus long term energy planning Considering temporal trade-offs in decarbonisation pathways University College London, 28 April 2016 Incorporating Flexibility into Long-term Energy
Workshop on Short term versus long term energy planning Considering temporal trade-offs in decarbonisation pathways University College London, 28 April 2016 Incorporating Flexibility into Long-term Energy
Siemens Solar Energy. Buenos Aires, November 2011 By Rolf Schumacher R2 Siemens AG All rights reserved
 Siemens Solar Energy Buenos Aires, November 2011 By Rolf Schumacher 2010-03-04-R2 Siemens has the answers to your burning questions 1 Why Solar / Renewable Energy? 2 What are the different technologies?
Siemens Solar Energy Buenos Aires, November 2011 By Rolf Schumacher 2010-03-04-R2 Siemens has the answers to your burning questions 1 Why Solar / Renewable Energy? 2 What are the different technologies?
Beyond LCOE: The Value of CSP with Thermal Energy Storage
 CSP Beyond LCOE: The Value of CSP with Thermal Energy Storage energy.gov/sunshot Mark S. Mehos, Program Manager, CSP NREL Discussion SunShot and LCOE Understanding the Value of CSP with Thermal Energy
CSP Beyond LCOE: The Value of CSP with Thermal Energy Storage energy.gov/sunshot Mark S. Mehos, Program Manager, CSP NREL Discussion SunShot and LCOE Understanding the Value of CSP with Thermal Energy
Renewable Technologies in the Future NEM
 Renewable Technologies in the Future NEM 100% Renewables for Australia? Dr Jenny Riesz Australian Power Institute (API) Summer School Wednesday 24 th February 2016 Who am I? Overview 100% Renewables: Worth
Renewable Technologies in the Future NEM 100% Renewables for Australia? Dr Jenny Riesz Australian Power Institute (API) Summer School Wednesday 24 th February 2016 Who am I? Overview 100% Renewables: Worth
Fujii labotatory, Depertment of Nuclear Engineering and Management, University of Tokyo Tel :
 Evaluation of the Optimal Power Generation Mix with Regional Power Interchange considering Output Fluctuation of Photovoltaic System and Power Generation Fujii labotatory, Depertment of Engineering and
Evaluation of the Optimal Power Generation Mix with Regional Power Interchange considering Output Fluctuation of Photovoltaic System and Power Generation Fujii labotatory, Depertment of Engineering and
Capacity Value of Concentrating Solar Power Plants
 Capacity Value of Concentrating Solar Power Plants Seyed Hossein Madaeni and Ramteen Sioshansi Ohio State University Paul Denholm National Renewable Energy Laboratory NREL is a national laboratory of the
Capacity Value of Concentrating Solar Power Plants Seyed Hossein Madaeni and Ramteen Sioshansi Ohio State University Paul Denholm National Renewable Energy Laboratory NREL is a national laboratory of the
Analysis of RES production diagram, a comparison of different approaches
 POSTER 2015, PRAGUE MAY 14 1 Analysis of RES production diagram, a comparison of different approaches Michaela Hrochová 1 1 Dept. of Economics, Management and Humanities, Czech Technical University, Technická
POSTER 2015, PRAGUE MAY 14 1 Analysis of RES production diagram, a comparison of different approaches Michaela Hrochová 1 1 Dept. of Economics, Management and Humanities, Czech Technical University, Technická
Why does a wind turbine have three blades?
 Why does a wind turbine have three blades? 1980 Monopteros 1983 Growian 1982 Darrieus Page 1 Why does a wind turbine have three blades? 1. It is because they look nicer? 2. Or because three blades are
Why does a wind turbine have three blades? 1980 Monopteros 1983 Growian 1982 Darrieus Page 1 Why does a wind turbine have three blades? 1. It is because they look nicer? 2. Or because three blades are
Testing of a Predictive Control Strategy for Balancing Renewable Sources in a Microgrid
 Testing of a Predictive Control Strategy for Balancing Renewable Sources in a Microgrid Mattia Marinelli; matm@elektro.dtu.dk Center for Electric Power and Energy DTU Risø Campus University of California
Testing of a Predictive Control Strategy for Balancing Renewable Sources in a Microgrid Mattia Marinelli; matm@elektro.dtu.dk Center for Electric Power and Energy DTU Risø Campus University of California
QUANTIFYING THE ACCURACY OF THE USE OF MEASURE-CORRELATE-PREDICT METHODOLOGY FOR LONG-TERM SOLAR RESOURCE ESTIMATES
 QUANTIFYING THE ACCURACY OF THE USE OF MEASURE-CORRELATE-PREDICT METHODOLOGY FOR LONG-TERM SOLAR RESOURCE ESTIMATES Christopher Thuman Marie Schnitzer Peter Johnson AWS Truepower, LLC 463 New Karner Road
QUANTIFYING THE ACCURACY OF THE USE OF MEASURE-CORRELATE-PREDICT METHODOLOGY FOR LONG-TERM SOLAR RESOURCE ESTIMATES Christopher Thuman Marie Schnitzer Peter Johnson AWS Truepower, LLC 463 New Karner Road
Integrating Renewables into the Power Grid
 Integrating Renewables into the Power Grid An Overview by Barney Speckman November 2010 Energy Solutions Overview Why do we have to integrate renewables What is meant by integrating renewables How does
Integrating Renewables into the Power Grid An Overview by Barney Speckman November 2010 Energy Solutions Overview Why do we have to integrate renewables What is meant by integrating renewables How does
Production Cost Modeling for High Levels of Photovoltaics Penetration
 National Renewable Energy Laboratory Innovation for Our Energy Future A national laboratory of the U.S. Department of Energy Office of Energy Efficiency & Renewable Energy Production Cost Modeling for
National Renewable Energy Laboratory Innovation for Our Energy Future A national laboratory of the U.S. Department of Energy Office of Energy Efficiency & Renewable Energy Production Cost Modeling for
Variability and uncertainty of wind power in the California electric power system
 WIND ENERGY Wind Energ. 2014; 17:1411 1424 Published online 13 June 2013 in Wiley Online Library (wileyonlinelibrary.com)..1640 RESEARCH ARTICLE Variability and uncertainty of wind power in the California
WIND ENERGY Wind Energ. 2014; 17:1411 1424 Published online 13 June 2013 in Wiley Online Library (wileyonlinelibrary.com)..1640 RESEARCH ARTICLE Variability and uncertainty of wind power in the California
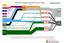 The Climate Change Problem Electricity generation is the main source of carbon emissions (25% of carbon emissions globally), followed by deforestation & land use (24%), industry (21%) and transportation
The Climate Change Problem Electricity generation is the main source of carbon emissions (25% of carbon emissions globally), followed by deforestation & land use (24%), industry (21%) and transportation
BEFORE THE PUBLIC UTILITIES COMMISSION OF THE STATE OF CALIFORNIA CALIFORNIA INDEPENDENT SYSTEM OPERATOR CORPORATION DETERMINISTIC STUDIES
 BEFORE THE PUBLIC UTILITIES COMMISSION OF THE STATE OF CALIFORNIA Order Instituting Rulemaking to Integrate and Refine Procurement Policies and Consider Long Term Procurement Plans Rulemaking 13 12 010
BEFORE THE PUBLIC UTILITIES COMMISSION OF THE STATE OF CALIFORNIA Order Instituting Rulemaking to Integrate and Refine Procurement Policies and Consider Long Term Procurement Plans Rulemaking 13 12 010
Evolution of the Grid in MISO Region. Jordan Bakke, David Duebner, Durgesh Manjure, Laura Rauch MIPSYCON November 7, 2017
 Evolution of the Grid in MISO Region Jordan Bakke, David Duebner, Durgesh Manjure, Laura Rauch MIPSYCON November 7, 2017 1 MISO s mission is to ensure reliable delivery of low-cost energy through efficient,
Evolution of the Grid in MISO Region Jordan Bakke, David Duebner, Durgesh Manjure, Laura Rauch MIPSYCON November 7, 2017 1 MISO s mission is to ensure reliable delivery of low-cost energy through efficient,
Envisioning a Renewable Electricity Future for the United States
 Envisioning a Renewable Electricity Future for the United States Trieu Mai, Ph.D. GCEP Net Energy Analysis Workshop April 1, 215 Stanford University, CA NREL is a national laboratory of the U.S. Department
Envisioning a Renewable Electricity Future for the United States Trieu Mai, Ph.D. GCEP Net Energy Analysis Workshop April 1, 215 Stanford University, CA NREL is a national laboratory of the U.S. Department
ASCEND OPTIMAL RESOURCE ANALYSIS
 ASCEND OPTIMAL RESOURCE ANALYSIS Prepared Submitted By: by: Ascend Analytics Ascend Analytics 1877 Broadway December 16, 2016 Suite 1877706 Broadway St, Suite 706 January 18, 2011 Boulder, CO 80302 Boulder,
ASCEND OPTIMAL RESOURCE ANALYSIS Prepared Submitted By: by: Ascend Analytics Ascend Analytics 1877 Broadway December 16, 2016 Suite 1877706 Broadway St, Suite 706 January 18, 2011 Boulder, CO 80302 Boulder,
Executive summary. Value of Smart Power Generation for utilities in Australia. A white paper by Wärtsilä and Roam Consulting
 Value of Smart Power Generation for utilities in Australia A white paper by Wärtsilä and Roam Consulting Executive summary This study analyses the potential of Smart Power Generation () power plants in
Value of Smart Power Generation for utilities in Australia A white paper by Wärtsilä and Roam Consulting Executive summary This study analyses the potential of Smart Power Generation () power plants in
Stepped Constraint Parameters. Issue Paper
 Stepped Constraint Parameters May 5, 2016 Table of Contents 1. Introduction... 3 2. Plan for Stakeholder Engagement... 4 3. Transmission constraint relaxation parameter... 5 4. Shift factor effectiveness
Stepped Constraint Parameters May 5, 2016 Table of Contents 1. Introduction... 3 2. Plan for Stakeholder Engagement... 4 3. Transmission constraint relaxation parameter... 5 4. Shift factor effectiveness
Demand Dispatch and Probabilistic Wind Power Forecasting in Unit Commitment and Economic Dispatch: A Case Study of Illinois
 1 Demand Dispatch and Probabilistic Wind Power Forecasting in Unit Commitment and Economic Dispatch: A Case Study of Illinois Zhi Zhou*, Audun Botterud Computational Engineer Argonne National Laboratory
1 Demand Dispatch and Probabilistic Wind Power Forecasting in Unit Commitment and Economic Dispatch: A Case Study of Illinois Zhi Zhou*, Audun Botterud Computational Engineer Argonne National Laboratory
DESIGN AND EXPERIMENT OF PARABOLIC TROUGH COLLECTOR WITH NORTH-SOUTH ORIENTATION
 DESIGN AND EXPERIMENT OF PARABOLIC TROUGH COLLECTOR WITH NORTH-SOUTH ORIENTATION Mr. Shailesh Prajapati 1 and Mr. Dip Shah 2 1,2 Assistant Proffesor,Mechanical Enginnering Department,Institute of Technolgy
DESIGN AND EXPERIMENT OF PARABOLIC TROUGH COLLECTOR WITH NORTH-SOUTH ORIENTATION Mr. Shailesh Prajapati 1 and Mr. Dip Shah 2 1,2 Assistant Proffesor,Mechanical Enginnering Department,Institute of Technolgy
Calculation models for the diffuse fraction of global solar radiation
 Calculation models for the diffuse fraction of global solar radiation Department of Building Physics & Building Ecology Vienna University of Technology Department of Building Physics & Building Ecology,
Calculation models for the diffuse fraction of global solar radiation Department of Building Physics & Building Ecology Vienna University of Technology Department of Building Physics & Building Ecology,
Game-Based Simulation of Gas-Fired Generation Mix With High Renewable Energy Shares
 Game-Based Simulation of Gas-Fired Generation Mix With High Renewable Energy Shares Mark Thurber Associate Director, Program on Energy and Sustainable Development Stanford University NGI Annual Affiliates
Game-Based Simulation of Gas-Fired Generation Mix With High Renewable Energy Shares Mark Thurber Associate Director, Program on Energy and Sustainable Development Stanford University NGI Annual Affiliates
Future Concepts in Solar Thermal Electricity Technology. Marc Röger. World Renewable Energy Congress XIV Bucharest, Romania, June 08-12, 2015
 Future Concepts in Solar Thermal Electricity Technology Marc Röger World Renewable Energy Congress XIV Bucharest, Romania, June 08-12, 2015 www.dlr.de Chart 2 > Future Concepts in Solar Thermal Electricity
Future Concepts in Solar Thermal Electricity Technology Marc Röger World Renewable Energy Congress XIV Bucharest, Romania, June 08-12, 2015 www.dlr.de Chart 2 > Future Concepts in Solar Thermal Electricity
On the Path to SunShot: Emerging Issues and Challenges in Integrating High Levels of Solar into the Electrical Generation and Transmission System
 On the Path to SunShot: Emerging Issues and Challenges in Integrating High Levels of Solar into the Electrical Generation and Transmission System Paul Denholm, Kara Clark, and Matt O Connell National Renewable
On the Path to SunShot: Emerging Issues and Challenges in Integrating High Levels of Solar into the Electrical Generation and Transmission System Paul Denholm, Kara Clark, and Matt O Connell National Renewable
Old and new uncertainly in power system
 Old and new uncertainly in power system Math Bollen Luleå University of Technology, Skellefteå 29 September 2016 1 Old and new uncertainty in power systems Uncertainty, intermittency, probability Hosting
Old and new uncertainly in power system Math Bollen Luleå University of Technology, Skellefteå 29 September 2016 1 Old and new uncertainty in power systems Uncertainty, intermittency, probability Hosting
Influence of Natural Gas Price and Other Factors on ISO-NE Electricity Price
 Influence of Natural Gas Price and Other Factors on ISO-NE Electricity Price Final Report for Undergraduate Research Opportunities Program Prepared by: Christiane Adcock, Milos Cvetkovic, Anuradha Annaswamy
Influence of Natural Gas Price and Other Factors on ISO-NE Electricity Price Final Report for Undergraduate Research Opportunities Program Prepared by: Christiane Adcock, Milos Cvetkovic, Anuradha Annaswamy
ISO Transmission Planning Process. Supplemental Sensitivity Analysis: Benefits Analysis of Large Energy Storage
 ISO 2016-2017 Transmission Planning Process Supplemental Sensitivity Analysis: Benefits Analysis of Large Energy Storage January 4, 2018 Contents 1. Introduction... 1 2. Background... 1 3. Objectives of
ISO 2016-2017 Transmission Planning Process Supplemental Sensitivity Analysis: Benefits Analysis of Large Energy Storage January 4, 2018 Contents 1. Introduction... 1 2. Background... 1 3. Objectives of
AR No. # Solar Thermal. Assessment Recommendation Savings Summary Source. Cost Savings Natural Gas. $984 * 1 MMBtu = 1,000,000 Btu
 AR No. # Solar Thermal Recommendation We recommend installing a solar thermal array on the building roof. This will provide an alternative source for 9.8% of the facilities energy consumption and reduce
AR No. # Solar Thermal Recommendation We recommend installing a solar thermal array on the building roof. This will provide an alternative source for 9.8% of the facilities energy consumption and reduce
INTEGRATION OF RENEWABLE BASED GENERATION INTO SRI LANKAN GRID
 CEYLON ELECTRICITY BOARD INTEGRATION OF RENEWABLE BASED GENERATION INTO SRI LANKAN GRID 2018-2028 Dr. H.M Wijekoon Chief Engineer (Transmission Planning) Randika Wijekoon Electrical Engineer (Generation
CEYLON ELECTRICITY BOARD INTEGRATION OF RENEWABLE BASED GENERATION INTO SRI LANKAN GRID 2018-2028 Dr. H.M Wijekoon Chief Engineer (Transmission Planning) Randika Wijekoon Electrical Engineer (Generation
Intercomparison between Switch 2.0 and GE MAPS for simulation of high-renewable power systems in Hawaii SUPPLEMENTARY INFORMATION
 Matthias Fripp, Supplementary Information page 1 of 8 Intercomparison between Switch 2.0 and GE MAPS for simulation of high-renewable power systems in Hawaii SUPPLEMENTARY INFORMATION Matthias Fripp 1,*
Matthias Fripp, Supplementary Information page 1 of 8 Intercomparison between Switch 2.0 and GE MAPS for simulation of high-renewable power systems in Hawaii SUPPLEMENTARY INFORMATION Matthias Fripp 1,*
Least-cost options for integrating intermittent renewables
 Copernicus Institute of Sustainable Development Least-cost options for integrating intermittent renewables Anne Sjoerd Brouwer 22-1-216 Introduction Stricter climate policies increasingly likely Power
Copernicus Institute of Sustainable Development Least-cost options for integrating intermittent renewables Anne Sjoerd Brouwer 22-1-216 Introduction Stricter climate policies increasingly likely Power
An Interactive Real Time Control Scheme For the Future Grid Operation
 An Interactive Real Time Control Scheme For the Future Grid Operation Taiyou Yong China Electric Power Research Institute May 15, 2014 1 Disclaimer The views expressed in this presentation are completely
An Interactive Real Time Control Scheme For the Future Grid Operation Taiyou Yong China Electric Power Research Institute May 15, 2014 1 Disclaimer The views expressed in this presentation are completely
Concentrating Solar Systems Radiation Resources Measurements, Data, and Uncertainty
 Concentrating Solar Systems Radiation Resources Measurements, Data, and Uncertainty NREL Electricity, Resources, and Buildings System Integration Center Daryl Myers Resource Information and Forecasting
Concentrating Solar Systems Radiation Resources Measurements, Data, and Uncertainty NREL Electricity, Resources, and Buildings System Integration Center Daryl Myers Resource Information and Forecasting
Solar PV Performance and New Technologies in Northern Latitude Regions
 SAND2018-3727 C Photos placed in horizontal position with even amount of white space between photos and header Solar PV Performance and New Technologies in Northern Latitude Regions This material is based
SAND2018-3727 C Photos placed in horizontal position with even amount of white space between photos and header Solar PV Performance and New Technologies in Northern Latitude Regions This material is based
Solar Project Yield Assessment. Workshop on Solar Power Project Development, Sept 20-21, 2012
 Solar Project Yield Assessment Workshop on Solar Power Project Development, Sept 20-21, 2012 Firstgreen Consulting Pvt Ltd. B 1202 Millennium Plaza, Sec 27 Gurgaon 122002 1 Solar Radiation Components 2
Solar Project Yield Assessment Workshop on Solar Power Project Development, Sept 20-21, 2012 Firstgreen Consulting Pvt Ltd. B 1202 Millennium Plaza, Sec 27 Gurgaon 122002 1 Solar Radiation Components 2
[R]enewables 24/7 EXECUTIVE SUMMARY
![[R]enewables 24/7 EXECUTIVE SUMMARY [R]enewables 24/7 EXECUTIVE SUMMARY](/thumbs/91/106622492.jpg) [R]enewables 24/7 EXECUTIVE SUMMARY Infrastructure needed to save the climate Grids keep power systems working The electricity grid' is a collective name for all wires, transformers and infrastructure
[R]enewables 24/7 EXECUTIVE SUMMARY Infrastructure needed to save the climate Grids keep power systems working The electricity grid' is a collective name for all wires, transformers and infrastructure
<Annual International Association of Energy Economics (IAEE) Conference, Daegu, Korea June 2013>
 POWER GENERATION PORTFOLIO ANALYSIS WITH HIGH PENETRATIONS OF PHOTOVOLTAICS: IMPLICATIONS FOR ENERGY
POWER GENERATION PORTFOLIO ANALYSIS WITH HIGH PENETRATIONS OF PHOTOVOLTAICS: IMPLICATIONS FOR ENERGY
Bulk Energy Storage Resource Case Study Update with the 2016 LTPP Assumptions
 Bulk Energy Storage Resource Case Study Update with the 2016 LTPP Assumptions Shucheng Liu Principal, Market Development 2016-2017 Transmission Planning Process Stakeholder Meeting February 28, 2017 Page
Bulk Energy Storage Resource Case Study Update with the 2016 LTPP Assumptions Shucheng Liu Principal, Market Development 2016-2017 Transmission Planning Process Stakeholder Meeting February 28, 2017 Page
Table of contents. 1 Introduction System impacts of VRE deployment Technical flexibility assessment of case study regions...
 Table of contents Foreword................................................................................. 3 Acknowledgements...5 Executive summary...13 1 Introduction...21 Background...21 Context...21
Table of contents Foreword................................................................................. 3 Acknowledgements...5 Executive summary...13 1 Introduction...21 Background...21 Context...21
Dr. Matthias Fripp Hawaii Natural Energy Institute, University of Hawaii at Manoa
 Intermodel Comparison Between Switch 2.0 and GE MAPS: Evaluating a New Tool for Integrated Modeling of Electric Vehicles and High-Renewable Power Systems Dr. Matthias Fripp Hawaii Natural Energy Institute,
Intermodel Comparison Between Switch 2.0 and GE MAPS: Evaluating a New Tool for Integrated Modeling of Electric Vehicles and High-Renewable Power Systems Dr. Matthias Fripp Hawaii Natural Energy Institute,
Sustainable Energy Science and Engineering Center. Concentrating Collectors - Power Generation
 Concentrating Collectors - Power Generation Solar Dish-Engine SAIC System SAIC Dish-Sterling System in Phoenix, Arizona Source: Dish Sterling Systems - overview, Thomas Mancini, ASME Journal of Solar Energy
Concentrating Collectors - Power Generation Solar Dish-Engine SAIC System SAIC Dish-Sterling System in Phoenix, Arizona Source: Dish Sterling Systems - overview, Thomas Mancini, ASME Journal of Solar Energy
Capacity and Flexibility Needs under Higher Renewables
 Capacity and Flexibility Needs under Higher Renewables Project Deliverable October 1, 2015 Arne Olson, Partner Ana Mileva, Senior Consultant Elaine Hart, Managing Consultant Defining today s planning problem
Capacity and Flexibility Needs under Higher Renewables Project Deliverable October 1, 2015 Arne Olson, Partner Ana Mileva, Senior Consultant Elaine Hart, Managing Consultant Defining today s planning problem
The Study on Application of Integrated Solar Combined Cycle(ISCC) Power Generation System in Kuwait. Summary of Reports.
 Commissioned by the Ministry of Economy, Trade and Industry The Study on Application of Integrated Solar Combined Cycle(ISCC) Power Generation System in Kuwait Summary of Reports January, 2008 Japan External
Commissioned by the Ministry of Economy, Trade and Industry The Study on Application of Integrated Solar Combined Cycle(ISCC) Power Generation System in Kuwait Summary of Reports January, 2008 Japan External
Global Energy Storage Demand for a 100% Renewable Electricity Supply
 Global Energy Storage Demand for a 100% Renewable Electricity Supply Guido Pleßmann, Matthias Erdmann, Markus Hlusiak and Christian Breyer 8 th International Renewable Energy Storage Conference and Exhibition
Global Energy Storage Demand for a 100% Renewable Electricity Supply Guido Pleßmann, Matthias Erdmann, Markus Hlusiak and Christian Breyer 8 th International Renewable Energy Storage Conference and Exhibition
California s Solar Buildout: Implications for Electricity Markets in the West
 California s Solar Buildout: Implications for Electricity Markets in the West EPIS Electric Market Forecasting Conference Las Vegas, Nevada September 7, 2017 Arne Olson, Partner Agenda Report From the
California s Solar Buildout: Implications for Electricity Markets in the West EPIS Electric Market Forecasting Conference Las Vegas, Nevada September 7, 2017 Arne Olson, Partner Agenda Report From the
Performance Testing of A Parabolic Trough Collector Array
 Performance Testing of A Parabolic Trough Collector Array İbrahim Halil Yılmaz *, Hakan Hayta, Recep Yumrutaş, Mehmet Sait Söylemez Department of Mechanical Engineering University of Gaziantep, 27310 Gaziantep,
Performance Testing of A Parabolic Trough Collector Array İbrahim Halil Yılmaz *, Hakan Hayta, Recep Yumrutaş, Mehmet Sait Söylemez Department of Mechanical Engineering University of Gaziantep, 27310 Gaziantep,
Prof Wikus van Niekerk Director of CRSES Prof Frank Dinter Eskom Chair in CSP Stellenbosch University
 Prof Wikus van Niekerk Director of CRSES Prof Frank Dinter Eskom Chair in CSP Stellenbosch University Fact not fiction: The true potential of concentrating solar thermal power 19/05/14 Prof JL (Wikus)
Prof Wikus van Niekerk Director of CRSES Prof Frank Dinter Eskom Chair in CSP Stellenbosch University Fact not fiction: The true potential of concentrating solar thermal power 19/05/14 Prof JL (Wikus)
A FLEXIBLE MARKOV-CHAIN MODEL FOR SIMULATING DEMAND SIDE MANAGEMENT STRATEGIES WITH APPLICATIONS TO DISTRIBUTED PHOTOVOLTAICS
 A FLEXIBLE MARKOV-CHAIN MODEL FOR SIMULATING DEMAND SIDE MANAGEMENT STRATEGIES WITH APPLICATIONS TO DISTRIBUTED PHOTOVOLTAICS Joakim Munkhammar, Joakim Widén Uppsala University, Sweden Address: P.O. Box
A FLEXIBLE MARKOV-CHAIN MODEL FOR SIMULATING DEMAND SIDE MANAGEMENT STRATEGIES WITH APPLICATIONS TO DISTRIBUTED PHOTOVOLTAICS Joakim Munkhammar, Joakim Widén Uppsala University, Sweden Address: P.O. Box
The Role of Wind and Solar PV in Mitigating the Impact of Uncertainty in the Australian Electricity Industry
 The Role of Wind and Solar PV in Mitigating the Impact of Uncertainty in the Australian Electricity Industry P. Vithayasrichareon 1, J. Riesz 2, and I. MacGill 3 Centre for Energy and Environmental Markets,
The Role of Wind and Solar PV in Mitigating the Impact of Uncertainty in the Australian Electricity Industry P. Vithayasrichareon 1, J. Riesz 2, and I. MacGill 3 Centre for Energy and Environmental Markets,
Spatial and Temporal Scales of Solar Variability: Implications for Grid Integration of Utility-Scale Photovoltaic Plants
 Spatial and Temporal Scales of Solar Variability: Implications for Grid Integration of Utility-Scale Photovoltaic Plants Andrew Mills and Ryan Wiser Lawrence Berkeley National Laboratory Electricity Markets
Spatial and Temporal Scales of Solar Variability: Implications for Grid Integration of Utility-Scale Photovoltaic Plants Andrew Mills and Ryan Wiser Lawrence Berkeley National Laboratory Electricity Markets
POWER-SYSTEM-WIDE ANALYSIS OF THE BENEFITS OF RESERVE PROVISION FROM SOLAR PHOTOVOLTAICS IN SOUTH AFRICA
 POWER-SYSTEM-WIDE ANALYSIS OF THE BENEFITS OF RESERVE PROVISION FROM SOLAR PHOTOVOLTAICS IN SOUTH AFRICA Tobias Bischof-Niemz 1, Joanne Calitz 2, Jarrad G. Wright 3 1, 2, 3 Council for Scientific and Industrial
POWER-SYSTEM-WIDE ANALYSIS OF THE BENEFITS OF RESERVE PROVISION FROM SOLAR PHOTOVOLTAICS IN SOUTH AFRICA Tobias Bischof-Niemz 1, Joanne Calitz 2, Jarrad G. Wright 3 1, 2, 3 Council for Scientific and Industrial
Pacific Northwest Low Carbon Scenario Analysis
 Pacific Northwest Low Carbon Scenario Analysis Achieving Least-Cost Carbon Emissions Reductions in the Electricity Sector November 8, 2017 Arne Olson, Partner Nick Schlag, Sr. Managing Consultant Jasmine
Pacific Northwest Low Carbon Scenario Analysis Achieving Least-Cost Carbon Emissions Reductions in the Electricity Sector November 8, 2017 Arne Olson, Partner Nick Schlag, Sr. Managing Consultant Jasmine
Use of weather forecast for increasing the self-consumption rate of home solar systems: an Italian case study
 Use of weather forecast for increasing the self-consumption rate of home solar systems: an Italian case study Mario Petrollese *, Giorgio Cau, Daniele Cocco Department of Mechanical, Chemical and Materials
Use of weather forecast for increasing the self-consumption rate of home solar systems: an Italian case study Mario Petrollese *, Giorgio Cau, Daniele Cocco Department of Mechanical, Chemical and Materials
Managing Flexibility in MISO Markets
 Managing Flexibility in MISO Markets Clean Energy Regulatory Forum November 9, 2012 Outline Impacts of Variable Generation on Ancillary Services Dispatchable Intermittent Resources Introduction to Proposed
Managing Flexibility in MISO Markets Clean Energy Regulatory Forum November 9, 2012 Outline Impacts of Variable Generation on Ancillary Services Dispatchable Intermittent Resources Introduction to Proposed
SIZING CURVE FOR DESIGN OF ISOLATED POWER SYSTEMS
 SIZING CURVE FOR DESIGN OF ISOLATED POWER SYSTEMS Arun P, Rangan Banerjee and Santanu Bandyopadhyay * Energy Systems Engineering, IIT Bombay, Mumbai, 400076, India. * Corresponding author, Phone: 91-22-25767894,
SIZING CURVE FOR DESIGN OF ISOLATED POWER SYSTEMS Arun P, Rangan Banerjee and Santanu Bandyopadhyay * Energy Systems Engineering, IIT Bombay, Mumbai, 400076, India. * Corresponding author, Phone: 91-22-25767894,
Renewable Electricity Futures: An Investigation of 30 90% Renewable Power
 Renewable Electricity Futures: An Investigation of 30 90% Renewable Power Stanford Energy Forum November 2012 Renewable Electricity Futures Study (2012). Hand, M.M.; Baldwin, S.; DeMeo, E.; Reilly, J.M.;
Renewable Electricity Futures: An Investigation of 30 90% Renewable Power Stanford Energy Forum November 2012 Renewable Electricity Futures Study (2012). Hand, M.M.; Baldwin, S.; DeMeo, E.; Reilly, J.M.;
